Processing est un programme avec des fonctionnalités graphiques permettant de réaliser des animations, c’est ce que nous allons voir maintenant

Neuvième programme : mode réactif 2

Résultat

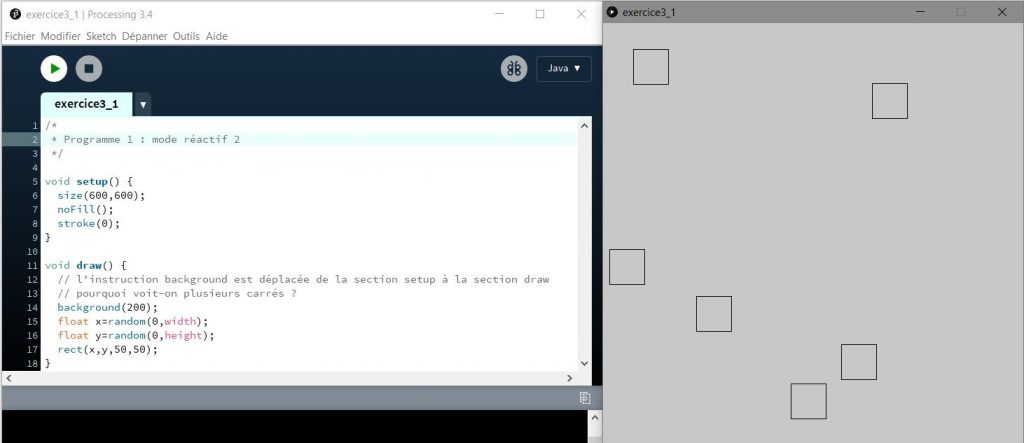
Code utilisé :

/*
* Programme 9 : mode réactif 2
*/
void setup() {
 size(600,600);
 noFill();
 stroke(0);
}
void draw() {
  background(200);
  float x=random(0,width);
  float y=random(0,height);
  rect(x,y,50,50);
}

Analyse du code, remarquez :

• Il s’agit du même programme que le quatrième de la première séquence avec une légère modification, l’avez-vous remarqué ?
• L’instruction background est déplacée de la fonction setup() à la fonction draw(), l’écran est donc effacé à chaque nouveau carré, on devrait alors ne voir qu’un seul carré à l’écran à la fois, pourquoi en voit-on plusieurs ?

Il s’agit du phénomène appelé “persistance rétinienne”, c’est à dire la capacité de l’œil (et du cerveau) à superposer une image déjà vue aux images que l’on est en train de voir. Cette propriété de l’œil est utilisée par le cinéma et la télévision pour donner l’impression d’un mouvement continu à partir d’une séquence d’images. La persistance est de l’ordre de 1/25ème de seconde, d’où la vitesse de diffusion des films fréquemment prévue autour de 25 images par seconde.

Dixième programme : animation brownienne

Dans le programme précédent le placement du rectangle est aléatoire. Il est donc incohérent s’il s’agit d’illustrer comment réaliser une animation. Dans ce programme un cercle va être déplacé depuis sa position initiale en suivant un trajet aléatoire (mouvement brownien). Le mouvement est rendu cohérent du fait que chaque position est définie non par rapport au plan entier de l’écran mais par un léger déplacement par rapport à la position précédente du cercle.

Résultat

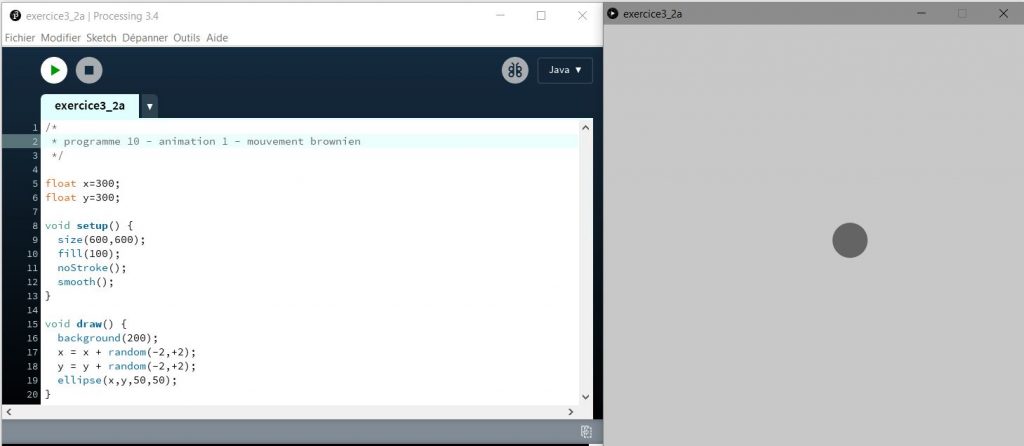
Code utilisé :

/*
 * programme 10 - animation 1 - mouvement brownien
 */
float x=300;
float y=300;
void setup() {
  size(600,600);
  fill(100);
  noStroke();
  smooth();
}
void draw() {
  background(200);
  x = x + random(-2,+2);
  y = y + random(-2,+2);
  ellipse(x,y,50,50);
}

Analyse du code, remarquez :

• La valeur des coordonnées x et y du point est définie par rapport à la position précédente.
• La valeur aléatoire du déplacement est entre des bornes assez petites.

Dixième programme – variante

A partir du programme précédent, réalisation d’un effet de foule, on appelle ça l’animation particulaire dans le jargon de l’animation par ordinateur. Dans ce type de cas il est préférable d’adopter une programmation orientée objet.

Notez que dans cet exemple, le mouvement des points n’est pas confiné, ils peuvent sortir de l’écran. De plus les collisions entre point ne sont pas gérées, à vous de compléter le programme !

Classe Particule

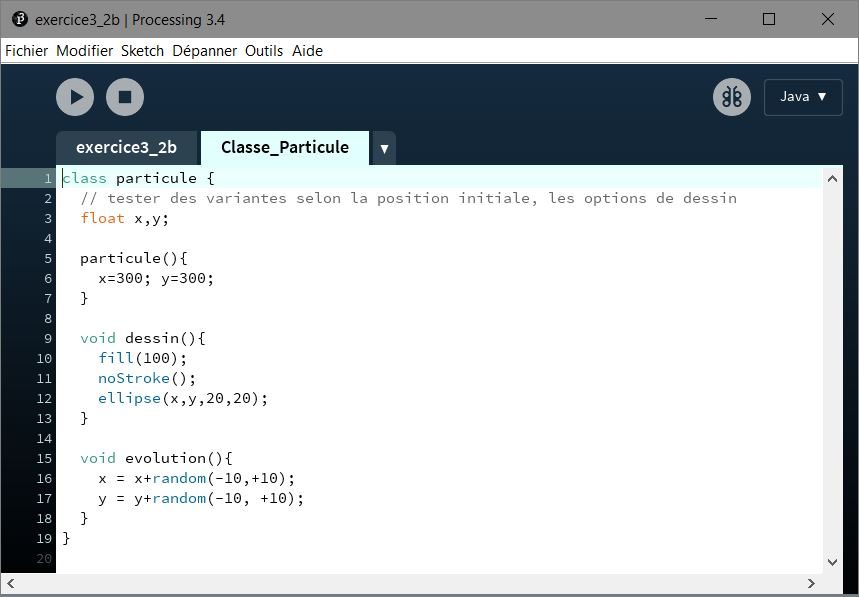
Code utilisé :

class Particule {
  float x,y;
  Particule(){
    x=300; y=300;
 }
  void dessin(){
    fill(100);
    noStroke();
    ellipse(x,y,20,20);
 }
  void evolution(){
    x = x+random(-10,+10);
    y = y+random(-10, +10);
  }
}

Résultat

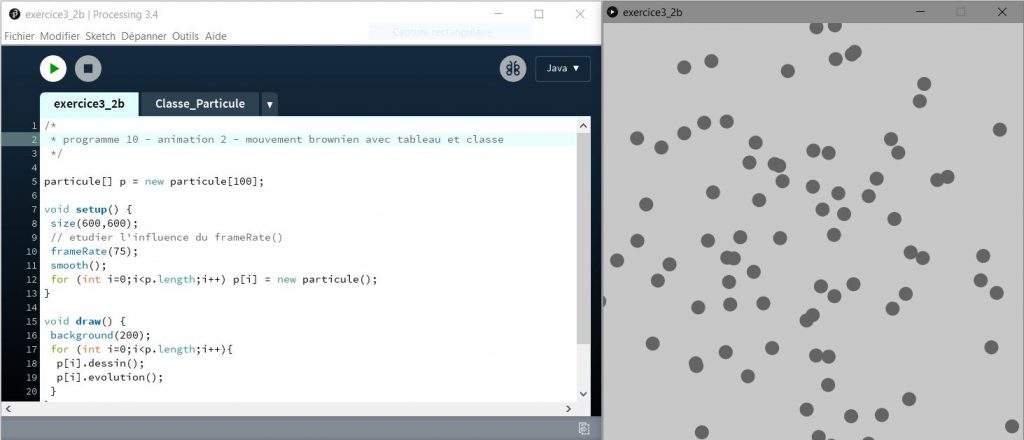
Code utilisé :

/*
 * programme 10 - animation 2 - mouvement brownien avec tableau et classe
 */
Particule[] p = new Particule[100];
void setup() {
  size(600,600);
  smooth();
  for (int i=0; i<p.length; i++) p[i] = new Particule();
}
void draw() {
  background(200);
  for (int i=0; i<p.length; i++){
    p[i].dessin();
    p[i].evolution();
  }
}

Analyse du code, remarquez :

• Une nouvelle fonctionnalité très courante et pratique pour traiter des éléments en nombre, l’utilisation d’un tableau.
• Les tableaux peuvent avoir autant de dimensions que nécessaire, celui-ci n’a qu’une dimension, on le note tableau[], un tableau à 2 dimensions se note tableau[][], etc.
• Le tableau est d’abord déclaré, ici il contient 100 éléments.
• Ensuite est créé l’espace mémoire nécessaire à la manipulation des objets, dans la fonction setup().
• Enfin dans la boucle de la fonction draw() le tableau est parcouru pour afficher et déplacer chacun des éléments.

Onzième programme : boulet

Nous allons réaliser une animation basée sur la physique des objets, la trajectoire parabolique d’un boulet de canon.

Un peu de physique

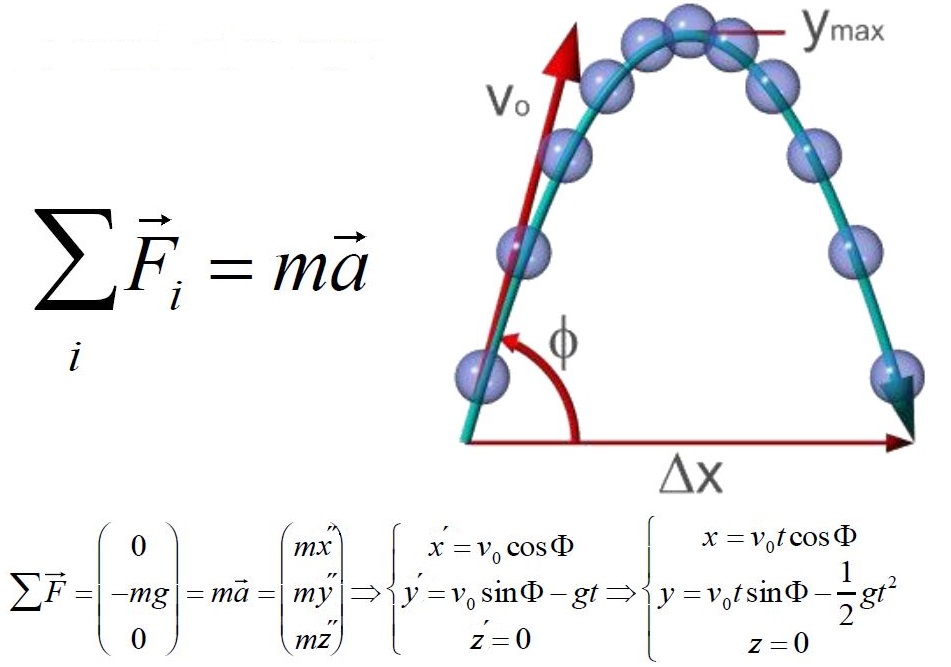
Théorème fondamental de la dynamique : pour un objet isolé, la somme des forces extérieures qu’il subit est égale à sa masse multipliée par son accélération.

Cet algorithme nous permet à partir de l’estimation de l’accélération d’un objet de déduire par intégration, sa vitesse, puis par une nouvelle intégration, ses coordonnées.

A partir de la masse d’un objet et des forces qu’il subit on peut donc prédire sa trajectoire.

Le boulet de canon est tiré avec une vitesse v0 un angle initial de tir Φ, sa trajectoire si la seule force à prendre en compte est la gravité est une parabole. On va calculer les coordonnées successives du boulet avec un procédé simple d’intégration numérique.

Résultat

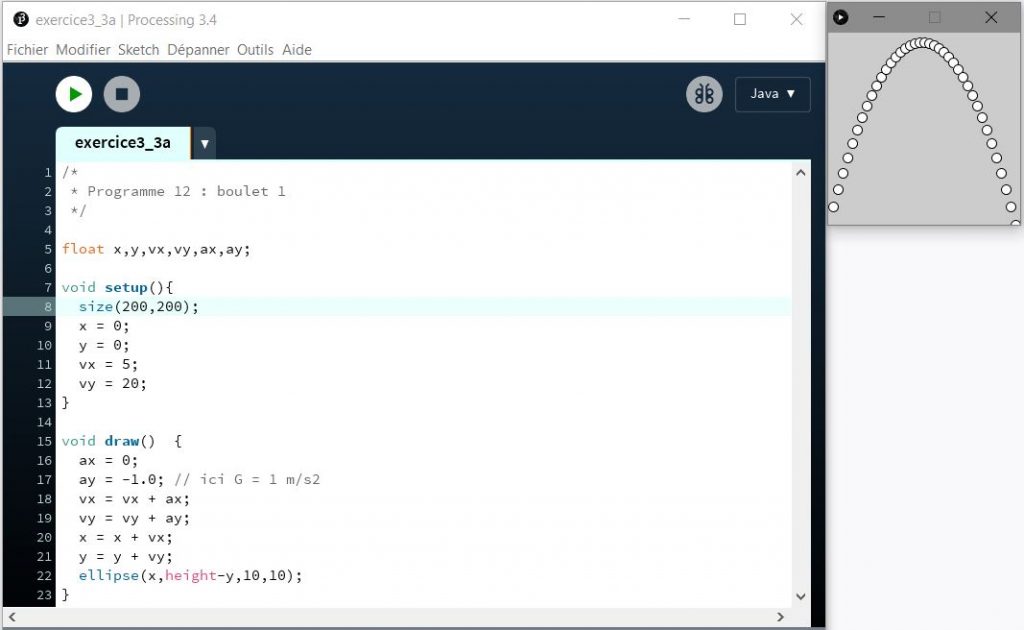
Code utilisé :

/*
 * Programme 11 : boulet 1
 */
float x,y,vx,vy,ax,ay;
void setup(){
  size(200,200);
  x = 0;
  y = 0;
  vx = 5;
  vy = 20;
}
void draw() {
  ax = 0;
  ay = -1.0; // ici G = 1 m/s2
  vx = vx + ax;
  vy = vy + ay;
  x = x + vx;
  y = y + vy;
  ellipse(x,height-y,10,10);
}

Analyse du code, remarquez :

La formule de calcul est simplifiée mais donne une belle parabole :

• La constante de gravitation est fixée à 1 m/s2 d’où la valeur ay = -1.0 (valeur décimale).
• Le facteur temps n’est pas exprimé, il correspond alors au frameRate c’est à dire à 1.
• La position du boulet est égale à chaque instant aux coordonnées précédentes auxquelles on ajoute le déplacement égal à la vitesse multipliée par le facteur temps.

Onzième programme – variante

Nous allons maintenant, toujours sur le programme du boulet, prendre en compte le sol et ajouter un effet de rebond.

Résultat

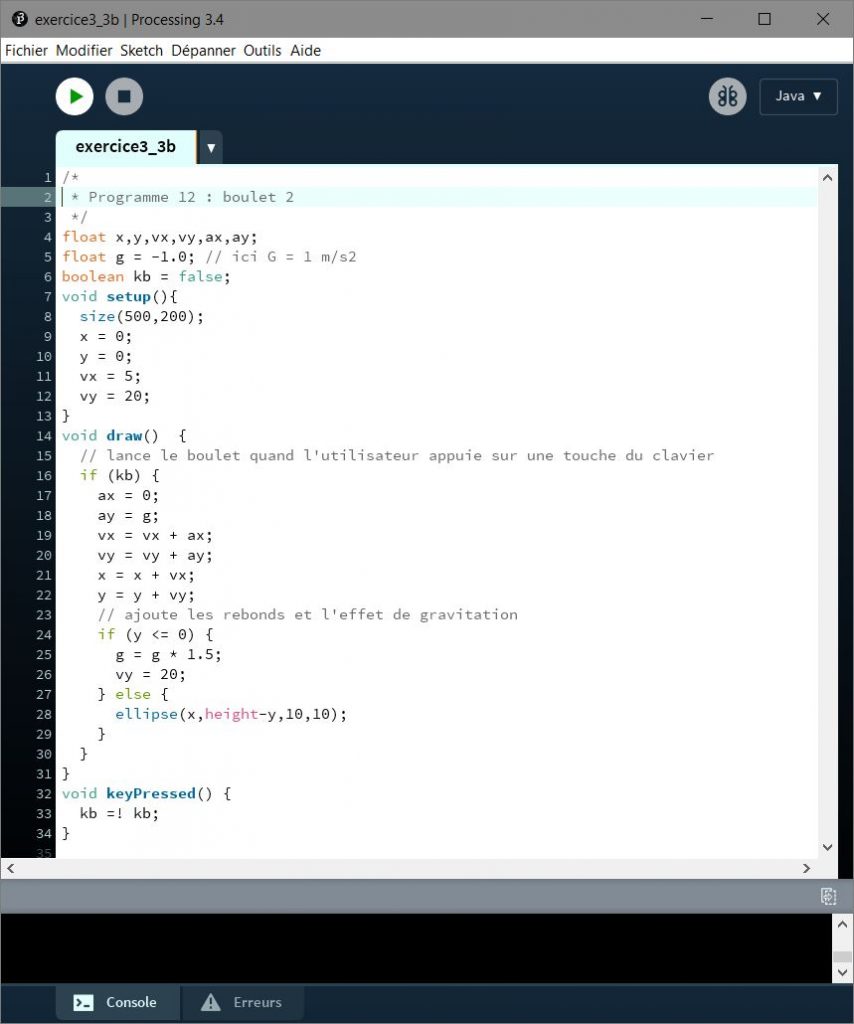
Code utilisé :

/*
 * Programme 11 : boulet 2
 */
float x,y,vx,vy,ax,ay;
float g = -1.0; // ici G = 1 m/s2
boolean kb = false;
void setup(){
  size(500,200);
  x = 0;
  y = 0;
  vx = 5;
  vy = 20;
}
void draw()  {
  // lance le boulet quand l'utilisateur appuie sur une touche du clavier
  if (kb) {
    ax = 0;
    ay = g;
    vx = vx + ax;
    vy = vy + ay;
    x = x + vx;
    y = y + vy;
    // ajoute les rebonds et l'effet de gravitation
    if (y <= 0) {
      g = g * 1.5;
      vy = 20;
    } else {
      ellipse(x,height-y,10,10);
    }
  }
}
void keyPressed() {
  kb =! kb;
}

Analyse du code, remarquez :

• Le lancement du boulet est provoqué lorsqu’une touche du clavier est pressée.
• Lorsque le boulet touche le sol il rebondit et perd de la vitesse (effet traduit par une augmentation de la gravité).
• kb est une variable booléenne, l’opérateur =! (opérateur logique NON) permet d’inverser sa valeur.

Douzième programme : particules

Cet effet inventé dans les années 1980 a fait les beaux jours de la synthèse d’images. Il a été appliqué pour la première fois par son inventeur Reeves dans le premier film de Star Trek ! Il s’agit d’une extension du tir parabolique appliqué à un grand nombre de particules.

Classe Particule

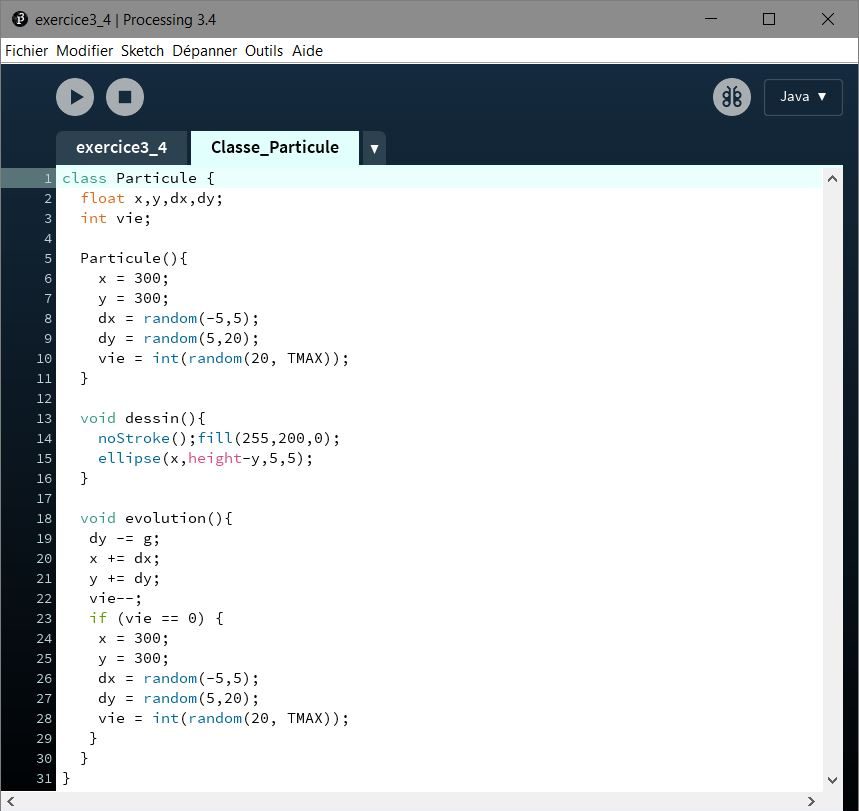
Code de la classe :

class Particule {
    float x,y,dx,dy;
    int vie;
    Particule(){
        x = 300;
        y = 300;
        dx = random(-5,5);
        dy = random(5,20);
        vie = int(random(20, TMAX));
    }
    void dessin(){
        noStroke();
        fill(255,200,0);
        ellipse(x,height-y,5,5);
    }
    void evolution(){
        dy -= g;
        x += dx;
        y += dy;
        vie--;
        if (vie == 0) {
            x = 300;
            y = 300;
            dx = random(-5,5);
            dy = random(5,20);
            vie = int(random(20, TMAX));
        }
    }
}

Résultat

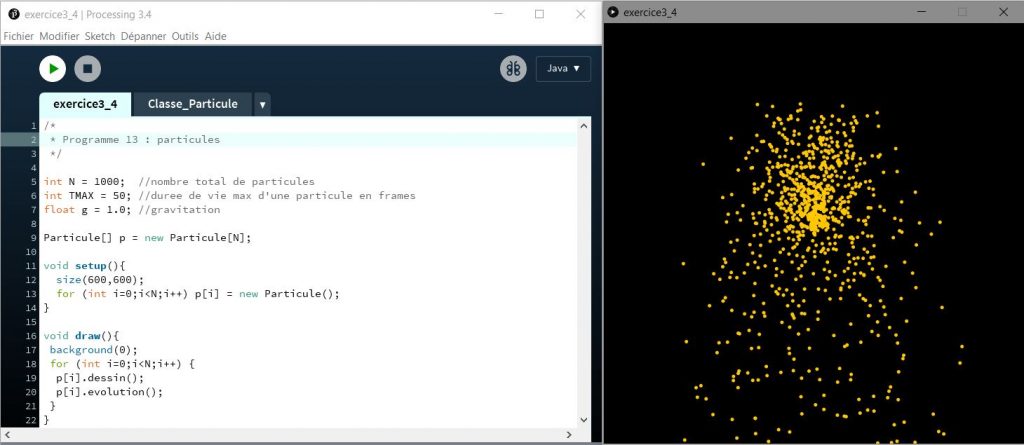
Code principal :

/*
 * Programme 12 : particules
 */
int N = 1000;  //nombre total de particules
int TMAX = 50; //durée de vie max d'une particule en frames
float g = 1.0; //gravitation
Particule[] p = new Particule[N];
void setup(){
    size(600,600);
    for (int i=0; i<N; i++) p[i] = new Particule();
}
void draw(){
    background(0);
    for (int i=0; i<N; i++) {
        p[i].dessin();
        p[i].evolution();
    }
}

Analyse du code, remarquez :

• Chaque particule suit une trajectoire de la même façon que le boulet précédemment.
• Chaque fois qu’une particule sort de l’écran elle est régénérée pour être lancée à nouveau.

Conclusion

De nombreux exemples sont fournis avec Processing, n’hésitez pas à les tester. A propos de la simulation de phénomènes physique comme le ressort, l’exercice s’appelle Spring.

Consultez aussi le site OpenProcessing, tourné vers l’utilisation artistique de Processing, qui propose biens des créations qui pourront vous inspirer.

Yves Durasnel
Club sympaTIC
Octobre 2018

Inspiré du FUN Mooc “Introduction aux technologies des médias interactifs numériques”
par Pierre Cubaud et Stéphane Natkin du CNAM